Ejemplos de Suma Algebraica

En álgebra la suma es una de las operaciones fundamentales y la más básica, sirve para sumar monomios y polinomios. La suma algebraica sirve para sumar el valor de dos o más expresiones algebraicas. Como se trata de expresiones que están compuestas por números, con literales y con exponentes, debemos estar atentos a las siguientes reglas:

Suma de monomios:

La suma de dos monomios puede dar como resultado un monomio o un polinomio.

Cuando los factores son iguales, por ejemplo, la suma 2x + 4x, el resultado será un monomio, ya que la literal es la misma y tiene el mismo grado (en este caso, sin exponente). En este caso sumaremos solo los términos numéricos, ya que, en ambos casos, es lo mismo que multiplicar por x:

2x + 4x = (2+4)x = 6x

Cuando las expresiones tienen signos diferentes, se respeta el signo. Si es necesario, escribimos la expresión entre paréntesis: (2x) + 4x; 4x + (2x). Aplicando la ley de los signos, al sumar una expresión conserva su signo, positivo o negativo:

4x + (2x) = 4x 2x = 2x

En el caso de que los monomios tengan literales diferentes, o en caso de tener la misma literal, pero con diferente grado (exponente), entonces el resultado de la suma algebraica es un polinomio, formado por los dos sumandos. Para distinguir la suma de su resultado, podemos escribir los sumandos entre paréntesis:

(4x) + (3y) = 4x + 3y (a) + (2a²) + (3b) = a + 2a² + 3b (3m) + (6n) = 3m 6n

Cuando en la suma hay dos o más términos comunes, es decir, con las mismas literales y del mismo grado, se suman entre sí, y se escribe la suma con los demás términos:

(2a) + (6b²) + (3a²) + (4b²) + (7a) + (9a²)= [(2a) + (7a)] + [(3a²) + (9a²)] + [(6b²) + (4b²)] = [9a]+[ 6a²]+[ 10b²] = 9a + 6a² 10b²

^{10 ejemplos de suma algebraica de monomios}

1. 2x + 4x = (2 + 4)x = 6x

2. 5y - 3y = (5 - 3)y = 2y

3. 7z + 2z = (7 + 2)z = 9z

4. -3a + 6a = (-3 + 6)a = 3a

5. 4b - 9b = (4 - 9)b = -5b

6. 8c + 5c = (8 + 5)c = 13c

7. 3d - 6d = (3 - 6)d = -3d

8. 6e + 7e = (6 + 7)e = 13e

9. 5f - 2f = (5 - 2)f = 3f

10. 9g + 4g = (9 + 4)g = 13g

En estos ejemplos podemos ver como se suman números enteros.

Suma de polinomios:

Un polinomio es una expresión algebraica que está formada por sumas y restas de los diferentes términos que conforman el polinomio. Para sumar dos polinomios, podemos seguir los siguientes pasos:

Sumaremos 3a2 + 4a + 6b 5c 8b2 con c + 6b2 3a + 5b

1. Ordenamos los polinomios en relación a sus números, sus letras y sus grados, respetando el signo de cada término:

3a2 + 4a + 6b 8b2 5c -3a + 6b2 + 5b + c

2. Agrupamos las sumas de los términos comunes: 

[3a2] + [4a 3a] + [6b + 5b] + [ 8b2 + 6b2] + [-5c + c]

2. Efectuamos las sumas de los términos comunes que pusimos entre paréntesis o corchetes. Recordemos que al ser suma, cata término del polinomio conserva su signo en el resultado:

[3a2] + [4a 3a] + [6b + 5b] + [ 8b2 + 6b2] + [-5c + c] = 3a2 + a + 11b 2b2 + (-4c)

Otra forma de ilustrar esto, es haciendo la suma en forma vertical, alineando los términos comunes y realizando las operaciones:

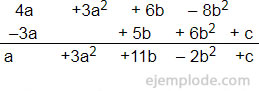
Suma de monomios y polinomios: Como podemos deducir de lo ya explicado, para sumar un monomio con un polinomio, seguiremos las reglas revisadas. Si existen términos comunes, el monomio se sumará al término; si no hay términos comunes, el monomio se agrega al polinomio como un término más:

Si tenemos (2x + 3x² 4y) + (4x²) Alineamos los términos comunes y realizamos la suma:

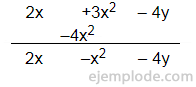
Si tenemos (m 2n² + 3p) + (4n), realizamos la suma, alineando los términos:

m                     2n²    + 3p           4n                              m         +4n      2n²     +3p

Es recomendable ordenar los términos de un polinomio, para facilitar su identificación y los cálculos de cada operación.

• Te puede interesar: Resta algebraica

10 ejemplos de suma algebraica de polinomios

Veamos 10 ejemplos de sumas de números enteros.

1. (2x + 3y) + (4x - 5y) = 2x + 3y + 4x - 5y = (2x + 4x) + (3y - 5y) = 6x - 2y

2. (3a - 4b) + (2a + 5b) = 3a - 4b + 2a + 5b = (3a + 2a) + (-4b + 5b) = 5a + b

3. (5x - 7y) + (-2x + 3y) = 5x - 7y - 2x + 3y = (5x - 2x) + (-7y + 3y) = 3x - 4y

4. (4a + 6b) + (3a - 2b) = 4a + 6b + 3a - 2b = (4a + 3a) + (6b - 2b) = 7a + 4b

5. (7x - 3y) + (-5x + 8y) = 7x - 3y - 5x + 8y = (7x - 5x) + (-3y + 8y) = 2x + 5y

6. (8a + 5b) + (2a - 3b) = 8a + 5b + 2a - 3b = (8a + 2a) + (5b - 3b) = 10a + 2b

7. (9x + 4y) + (3x - 7y) = 9x + 4y + 3x - 7y = (9x + 3x) + (4y - 7y) = 12x - 3y

8. (6a - 7b) + (4a + 5b) = 6a - 7b + 4a + 5b = (6a + 4a) + (-7b + 5b) = 10a - 2b

9. (5x + 8y) + (-3x - 2y) = 5x + 8y - 3x - 2y = (5x - 3x) + (8y - 2y) = 2x + 6y

10. (7a + 9b) + (5a - 6b) = 7a + 9b + 5a - 6b = (7a + 5a) + (9b - 6b) = 12a + 3b

Suma algebraica de fracciones

La suma de dos fracciones puede dar como resultado una fracción o un número entero.

Cuando los denominadores son iguales, por ejemplo, la suma 3/5 + 2/5, el resultado será una fracción, ya que se puede sumar directamente los numeradores:

3/5 + 2/5 = (3+2)/5 = 5/5 = 1

Cuando los denominadores son diferentes, es necesario encontrar un denominador común antes de sumar las fracciones. Por ejemplo, al sumar 1/3 + 1/2, primero encontramos el mínimo común múltiplo (MCM) de los denominadores 3 y 2, que es 6:

1/3 + 1/2

Ahora ajustamos las fracciones para que tengan el mismo denominador (6):

(1/3) * (2/2) = 2/6 (1/2) * (3/3) = 3/6

Entonces, las fracciones ajustadas son:

2/6 + 3/6

Ya que los denominadores son iguales, podemos sumar los numeradores:

(2+3)/6 = 5/6

La fracción resultante es 5/6 y no se puede simplificar más.

Cuando se suman fracciones con números enteros, primero convertimos el número entero en una fracción con el mismo denominador que la otra fracción, luego sumamos las fracciones:

2 + 3/4

Primero convertimos el número entero 2 en una fracción con denominador 4:

2 * (4/4) = 8/4

Ahora sumamos las fracciones:

8/4 + 3/4 = (8+3)/4 = 11/4

La fracción resultante es 11/4, que también puede ser expresada como un número mixto: 2 3/4.

10 ejemplos de suma algebraica de fracciones

1. 1/3 + 1/4 = (4 + 3) / (3 * 4) = 7/12

2. 3/5 - 2/5 = (3 - 2) / 5 = 1/5

3. 5/6 + 1/3 = (5 + 2) / 6 = 7/6

4. 7/8 - 3/4 = (7 - 6) / 8 = 1/8

5. 2/9 + 4/9 = (2 + 4) / 9 = 6/9 = 2/3

6. 5/12 + 7/12 = (5 + 7) / 12 = 12/12 = 1

7. 3/7 - 1/7 = (3 - 1) / 7 = 2/7

8. 8/15 + 3/5 = (8 + 9) / 15 = 17/15

9. 1/2 - 1/4 = (2 - 1) / 4 = 1/4

10. 7/10 + 3/10 = (7 + 3) / 10 = 10/10 = 1

10 ejemplos de suma algebraica desarrollados

1. (2x + 3y) + (4x - 5y) = 2x + 3y + 4x - 5y = (2x + 4x) + (3y - 5y) = 6x - 2y

2. (3a^2 - 4ab) + (2ab - 5a^2) = 3a^2 - 4ab + 2ab - 5a^2 = (3a^2 - 5a^2) + (-4ab + 2ab) = -2a^2 - 2ab

3. (5x^2y + 3xy^2) + (-2x^2y + 7xy^2) = 5x^2y + 3xy^2 - 2x^2y + 7xy^2 = (5x^2y - 2x^2y) + (3xy^2 + 7xy^2) = 3x^2y + 10xy^2

4. (8a - 3b + 5c) + (2a + 4b - 7c) = 8a - 3b + 5c + 2a + 4b - 7c = (8a + 2a) + (-3b + 4b) + (5c - 7c) = 10a + b - 2c

5. (4x^3 - 5x^2 + 2x) + (3x^3 + 2x^2 - x) = 4x^3 - 5x^2 + 2x + 3x^3 + 2x^2 - x = (4x^3 + 3x^3) + (-5x^2 + 2x^2) + (2x - x) = 7x^3 - 3x^2 + x

6. (9y^2z - 4yz^2) + (-3y^2z + 8yz^2) = 9y^2z - 4yz^2 - 3y^2z + 8yz^2 = (9y^2z - 3y^2z) + (-4yz^2 + 8yz^2) = 6y^2z + 4yz^2

7. (7ab^2 - 5a^2b) + (3ab^2 + 2a^2b) = 7ab^2 - 5a^2b + 3ab^2 + 2a^2b = (7ab^2 + 3ab^2) + (-5a^2b + 2a^2b) = 10ab^2 - 3a^2b

8. (6x^2 - 4xy) + (-3x^2 + 5xy) = 6x^2 - 4xy - 3x^2 + 5xy = (6x^2 - 3x^2) + (-4xy + 5xy) = 3x^2 + xy

9. (5p^3 - 8p^2 + 4p) + (-2p^3 + 3p^2 - p) = 5p^3 - 8p^2 + 4p - 2p^3 + 3p^2 - p = (5p^3 - 2p^3) + (-8p^2 + 3p^2) + (4p - p) = 3p^3 - 5p^2 + 3p

10. (4r^2s - 7rs^2 + 2s^3) + (3r^2s + 6rs^2 - s^3) = 4r^2s - 7rs^2 + 2s^3 + 3r^2s + 6rs^2 - s^3 = (4r^2s + 3r^2s) + (-7rs^2 + 6rs^2) + (2s^3 - s^3) = 7r^2s - rs^2 + s^3

30 Ejemplos de suma algebraica resueltos

1. (3x) + (4x) = 7x
2. (3x) + (4x) = x
3. (3x) + (4x) = x
4. (3x) + (4x) = 7x
5. (2x) + (2x²) = 2x + 2x²
6. (2x) + (2x²) = 2x + 2x²
7. (2x) + (2x²) = 2x 2x²
8. (2x) + (2x²) = 2x 2x²
9. (3m) + (4m²) + (4n) = 3m + 4m² + 4n
10. (3m) + (4m²) + (4n) = 3m 4m² + 4n
11. (3m) + (4m²) + (4n) = 3m 4m² 4n
12. (3m) + (4m²) + (4n) = 3m + 4m² + 4n
13. (2b² + 4c + 3a³) + (5a + 3b + c²) = 5a + 3a³ + 3b + 2b² + 4c + c²
14. (2b² + 4c + 3a³) + (5a + 3b c²) = 5a + 3a³ + 3b 2b² + 4c c²
15. (2b² + 4c 3a³) + (5a + 3b c²) = 5a 3a³ + 3b + 2b² + 4c c²
16. (2b² 4c + 3a³) + (5a + 3b + c²) = 5a + 3a³ + 3b + 2b² 4c + c²
17. (2b² + 4c + 3a³) + (5a + 3b + c²) = 5a + 3a³ + 3b + 2b² + 4c + c²
18. (2b² 4c 3a³) + (5a 3b c²) = 5a 3a³ 3b 2b² 4c c²
19. (4x² + 6y + 3y²) + (x + 3 x² + y²) = x + 7x² + 6y + 4y²
20. (4x² + 6y + 3y²) + (x + 3 x² + y²) = x x² + 6y + 4y²
21. (4x² + 6y + 3y²) + (x 3 x² + y²) = x + x² + 6y + 4y²
22. (4x² 6y 3y²) + (x + 3 x² + y²) = x + 7x² 6y 2y²
23. (4x² + 6y + 3y²) + (x + 3 x² y²) = x + 7x² + 6y + 2y²
24. (4x² 6y 3y²) + (x 3 x² y²) = x 7x² 6y 4y²
25. (x + y + 2z²) + (x + y + z²) = 2x + 2y + 3z²
26. (x + y + 2z²) + (x + y + z²) = 2y + 3z²
27. (x y + 2z²) + (x + y + z²) = 3z²
28. (x y 2z²) + (x + y + z²) = 2x z²
29. (x + y + 2z²) + (x + y z²) = 2y + z²
30. (x y 2z²) + (x y z²) = 2x 2y 3z²

Sigue con:

• Resta algebraica