Ejemplo de Unión De Conjuntos

Se sabe que un conjunto es un grupo de elementos que tienen una característica en común, por la cual se vuelve clara la diferencia con otros elementos y grupos. Los conjuntos han funcionado en matemáticas como un concepto que sirve para establecer estadísticas o medidas de la característica común. Por ejemplo, para contar cuántos elementos hay en cada conjunto, y comparar ambos conjuntos para ver cuál es mayor.

Se llama Universo a lo que contiene todo; dicho de otro modo, es lo que habitan todos los elementos que pueden agruparse y los que no se pueden agrupar. Dentro del Universo van a estar todos los conjuntos posibles y los elementos sueltos. El Universo se representará con un rectángulo, como señal de que tiene un límite, con todos los elementos dentro.

Para definir gráficamente un conjunto dentro del Universo, se traza un círculo en el interior del rectángulo y se escriben dentro de él todos los elementos que lo compongan. Los elementos que no tengan la característica común, se dejan escritos en el resto del área del rectángulo, indicando con esto que no pertenecen al conjunto definido.

Lo mismo se hará si hay segundo conjunto y tercero, para observar los círculos dentro del Universo, conteniendo sus respectivos elementos.

Pero llegará el momento en que dos o tres conjuntos posean elementos que cumplan con dos o tres características en común, dándose así la unión parcial de los conjuntos.

Diagrama de Venn

El Diagrama de Venn es la herramienta para representar la unión de conjuntos por excelencia. Los círculos de los conjuntos se solapan para generar un área intermedia, llamada Intersección, que es la que representa a los elementos que cumplen con las características de ambos conjuntos al mismo tiempo.

El Diagrama de Venn, para casos específicos, tiene como propósito ofrecer una ayuda gráfica a la hora de estimar el número de elementos en uno de los conjuntos cuando no se tengan todos los datos.

Ejemplos de Unión de conjuntos

Ejemplo de unión de dos conjuntos

Se tiene un grupo de 30 personas (universo), a quienes se pregunta si prefieren la Música Clásica o el género Rock. 10 responden que les gusta el Rock solamente, 4 prefieren la música clásica exclusivamente, y resulta que las otras 16 personas tienen un gusto igual por las dos. Los conjuntos y la intersección se representarían como sigue:

Ejemplo de unión de dos conjuntos de preferencias

Para hacer una encuesta en unas salas de cine sobre los sabores de palomitas preferidos, se tomó a 150 personas. Los sabores ofrecidos eran Mantequilla y Caramelo. De los encuestados, 70 en total respondieron con un gusto por las de Mantequilla. Si se reúnen 93 personas que tienen gusto por ambas, y son 20 las que tienen gusto únicamente por las de Caramelo, ya se puede descubrir cuántas tienen gusto exclusivo por las de Mantequilla, sin contar las de la intersección, y al final el número total de las que gustan por las de Caramelo. El diagrama queda así:

Para la solución de este diagrama, se colocan los datos dados en el problema. El número 70 de los que tienen gusto por las de Mantequilla lo colocamos junto al nombre del conjunto, para representar a su total. En la intersección irán las 93 personas que tienen gusto por ambos. Las 20 personas que tienen gusto exclusivo por el sabor Caramelo, irá en la sección de círculo que sólo indica Caramelo.

Sumando la Intersección = 93, y la sección Caramelo = 20, tenemos como resultado 113, que son los elementos hasta ahora contabilizados. Sabemos que el universo U = 150, son los elementos totales. La diferencia entre el Universo U = 150 y los elementos hasta ahora contados = 113, tenemos como resultado = 37, que son los elementos restantes, pertenecientes a la sección Mantequilla.

Para conocer los elementos totales en el conjunto Caramelo, primero conoceremos los elementos Mantequilla presentes en la intersección. Se sabe que son 70 elementos Mantequilla. Y 37 de ellos son de gusto único. La diferencia entre ellos es = 33. Son 33 elementos Mantequilla presentes en la Intersección. Así que ya podemos conocer el número de elementos Caramelo en la Intersección. 93 – 33 = 60. Son 60 elementos Caramelo encerrados en la Intersección. Sumados a los 20 de los Caramelo exclusivos, se sabrá que el conjunto Caramelo tiene en total: 60 + 20 = 80 elementos.

Ejemplo de unión de dos conjuntos de personas

Para un trabajo de investigación de adicciones, se estableció una encuesta para conocer el número de personas que fumaban, ingerían bebidas alcohólicas, o hacían ambos. El grupo que se manejó fue de 300 personas. Se tomó nota de que 203 personas convergían en una práctica doble de los vicios; 45 personas se dedicaban exclusivamente a Fumar. Y en el conjunto de los alcohólicos había 112 elementos. Así se representaría el caso actual:

Para resolver este caso, primero se puede conocer el número total de elementos en el conjunto Fumar. Si sabemos que el Universo consta de 300 personas, y ya hay 112 en el conjunto Alcohol, por diferencia podemos saber que son 300 – 112 = 188 personas en el conjunto Fumar.

Para conocer el número de elementos Fumar en la Intersección, sólo hacemos la diferencia de 188 totales menos los 45 exclusivos. 188 – 45 = 143. Hay 143 elementos Fumar en la Intersección.

De manera que, restándolos de los 203 elementos de la Intersección, quedan 203 – 143 = 60 elementos. Hay 60 elementos Alcohol en la Intersección. Gracias a este cálculo, y restando de los 112 totales, será posible conocer los elementos exclusivos de Alcohol.

112 – 60 = 52. Hay 52 personas que únicamente ingieren bebidas alcohólicas. Así, ya está resuelto el diagrama.

Ejemplo de unión de tres conjuntos 

En las ocasiones en que los conjuntos de trabajo son tres, se generarán más Intersecciones que los van a relacionar entre sí. Además, se originará una intersección general de los tres conjuntos en el centro del diagrama.

Se va a estudiar a un grupo de lectura, para conocer las preferencias literarias de sus integrantes, entre Novela, Cuento y Microrrelatos. El grupo o universo consta de 40 personas.

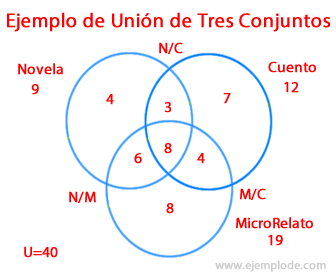
Los datos recolectados se han colocado en el Diagrama de Venn, repartido en su interior el universo de 40 personas. Se sabe entonces que 9 personas en total tienen gusto por la Novela, 12 por el Cuento y 19 por el MicroRelato. Dentro de estos tres conjuntos, 4 tienen un gusto exclusivo por la Novela, 7 tienen un gusto único por el Cuento, y 8 gustan sólo del MicroRelato.

Hay personas que tienen gusto por Novela y Cuento a la vez, que es la Intersección N/C = 3 personas. Los que gustan de Cuento y MicroRelato a la vez, la Intersección M/C son 4 personas. Y los que tienen un gusto simultáneo por Novela y MicroRelato, en la Intersección N/M, son 6 personas.

Finalmente, fueron 8 personas las que tenían un gusto por los tres conceptos al mismo tiempo.

Ejemplo de unión de tres cojuntos de preferencias

Un restaurante de buffet quiso ampliar su repertorio e hizo una encuesta con 250 clientes para ver qué preferencia mayoritaria había entre la comida japonesa, la comida mexicana y la comida italiana. El diagrama de Venn quedó como sigue:

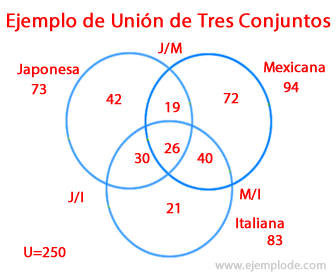
Interpretando el diagrama, el resultado fue el siguiente: hay 73 personas que tienen gusto por la comida japonesa, 94 personas con gusto por la comida mexicana, y 83 personas que tienen gusto por la comida italiana.

Hay personas que tienen gusto único por cada tipo de comida. Hay 42 personas a las que les gusta sólo la comida Japonesa. Hay 72 personas a las que les gusta sólo la comida Mexicana. Y hay 21 personas que tienen gusto por la comida Italiana únicamente.

Dentro de los conjuntos Japonesa, Mexicana e Italiana, hay personas que tienen gustos mixtos, que combinan ya sea dos de ellos o todos.

Hay 19 personas a las que les gustan las comidas Japonesa y Mexicana. Hay 40 personas a las que les gustan las comidas Mexicana e Italiana. Hay 30 personas a las que les gustan las comidas Japonesa e Italiana. Y hay 26 personas a las que les gustan las tres comidas, Japonesa, Mexicana e Italiana por igual.