Ejemplo de Ángulos

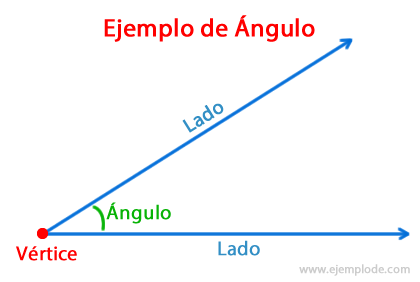
Un ángulo es la abertura comprendida entre dos semirrectas que se encuentran unidas en un mismo punto, formando una punta o Vértice. Esta abertura tiene una medida, que puede ser definida en dos sistemas diferentes: Grados Sexagesimales y Radianes, pero para definirlos es necesario abordar algunos conceptos antes.

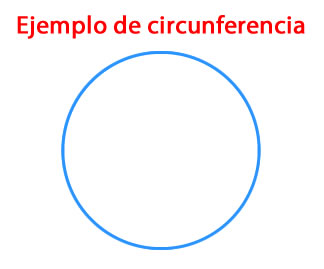
Circunferencia

Es una línea cuyos puntos se encuentran todos a la misma distancia de un centro. A la figura geométrica definida por esta línea se le llama Círculo.

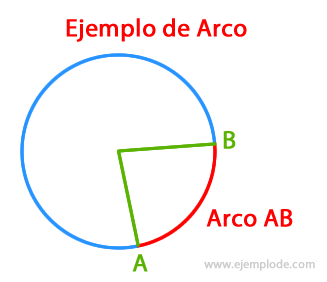
Arco

Es una porción de la Circunferencia con que se esté trabajando, delimitada por las dos líneas que forman un ángulo.

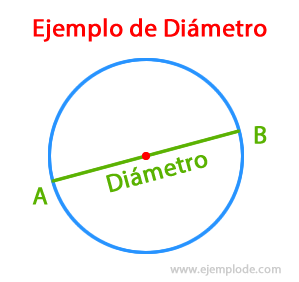
Diámetro

Es la distancia que hay entre un punto de la circunferencia y otro opuesto, pasando estrictamente por el centro.

Radio

Es la medida desde el centro de una circunferencia hasta cualquier punto del contorno. Equivale a la mitad del Diámetro.

El valor de π (Pi)

π (Pi) es una constante que corresponde al número de veces que cabe el Diámetro de una circunferencia en el Perímetro de la misma. Su valor hasta el sexto decimal es:

π = 3.141592...

De manera que, por ejemplo, el Radio cabe 2 π veces en la circunferencia.

Grados Sexagesimales

Los Grados Sexagesimales son un sistema de medición aplicado a la circunferencia, que consiste en separarla en 360 divisiones iguales o Grados. Todos los ángulos quedan comprendidos entre los 0° y los 360°.

El punto de partida fue el ángulo de 90°, que es la cuarta parte de la circunferencia. Se estableció que 1° correspondía a 1/90 del ángulo de 90°.

Además, se crearon dos medidas menores, para cuando un ángulo abarcara porciones menores a 1° entero. El Minuto, que corresponde a 1/60 de Grado. Y el Segundo, equivalente a 1/60 de Minuto.

Radianes

Radián es la medida que se asigna al ángulo cuyo Arco mide 1 Radio. A partir de esta declaración, es posible comenzar a esclarecer la conexión con los Grados Sexagesimales.

Se dedujo con anterioridad que el Radio cabe 2 π veces en la circunferencia completa, es decir, aproximadamente 6.28 veces en los 360°. Entonces se puede establecer la siguiente relación:

2 π radian = 360°

De manera que, despejando 1 radián:

1  radian = (360°/2π) = aprox 57°

Tipos de Ángulos

Comúnmente, los ángulos se clasifican de acuerdo con su medida. Los hay de las siguientes medidas:

Ángulo Agudo:

Son aquellos que miden menos de 90°. Consulta la información de los Ángulos Agudos.

Ángulo Recto:

Es aquel ángulo que mide exactamente 90°. Consulta la información de los Ángulos Rectos.

Ángulo Obtuso:

Son aquellos que miden más de 90°. Consulta la información de los Ángulos Obtusos.

Ángulo Llano:

Es aquel que mide exactamente 180°. Consulta la información del Ángulo Llano.

Ángulos opuestos por el vértice

Cuando dos rectas se cruzan, se forma un arreglo de cuatro ángulos, que sumados entre sí dan como resultado los 360°.

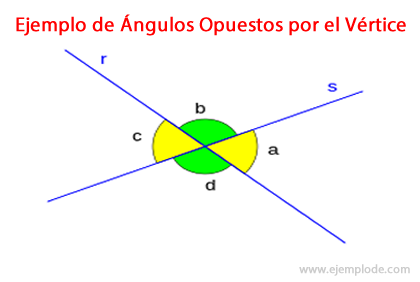
Arreglo de ángulos por el cruce de dos rectas.

 A cada ángulo corresponden las dos semirrectas que lo forman.

Los ángulos “b” y “d” se encuentran en posiciones opuestas, tomando como referencia el punto de cruce. A esto se llama que sean “opuestos por el vértice”. En el arreglo de ángulos hay simetría, por lo que “b” y “d” son de igual medida. Lo mismo ocurre con “a” y “c”, también opuestos por el vértice, y de misma magnitud.

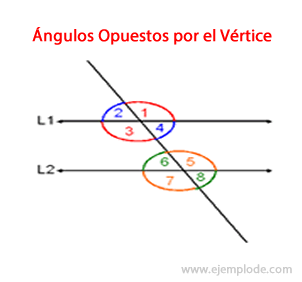
Ejemplo de Arreglo de Ángulos. Se presentan dos cruces, que generan sus dos pares de ángulos cada uno. Aquí hay que hacer la observación de que las rectas L1 y L2 son PARALELAS, es decir, tienen la misma pendiente o inclinación. Gracias a esta característica, y a que en cada arreglo de ángulos hay simetría, se concluye que los ángulos 1, 3, 5 y 7 tienen la misma medida. Y lo mismo ocurre con 2, 4, 6 y 8.

Gracias a que L1 y L2 son paralelas, y a que la recta de cruce conserva su inclinación, se generan dos sistemas de ángulos idénticos.

Ángulos Complementarios

Los ángulos complementarios son los que entre sí suman una medida de 90°. Pueden ser dos o más ángulos agudos. Si la suma excede los 90° o es menor, ya no se trata de ángulos complementarios.

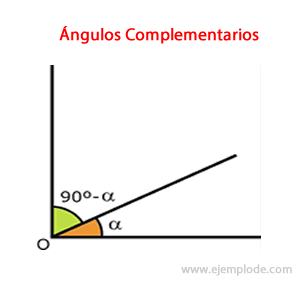
Regla que siguen los ángulos complementarios. Su suma siempre será 90°.

Ángulos Suplementarios

Los ángulos suplementarios son aquellos que entre sí suman 180°. Puede tratarse de dos o varios ángulos menores que conformen ese resultado. Si la suma excede los 180° o es menor, ya no se trata de ángulos suplementarios.

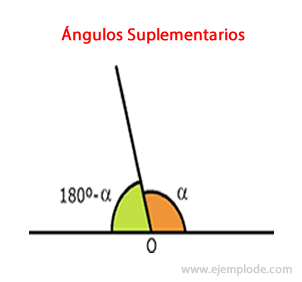Regla que siguen los ángulos suplementarios. Su suma siempre será 180°.