Teorema De Bernoulli

En Física, el Teorema de Bernoulli es el enunciado que nos describe las energías que están involucradas en el flujo de los líquidos a través de tuberías.

La Presión de un Líquido que fluye por una tubería es baja si su velocidad es alta. Por el contrario, esta Presión es elevada cuando el Líquido va despacio.

El Físico suizo Daniel Bernoulli enunció el siguiente teorema que lleva su nombre:

“En un líquido ideal cuyo flujo es estacionario, la suma de las Energías Cinética, Potencial y de Presión que tiene el líquido en un punto, es igual a la suma de estas energías en otro punto cualquiera”

El líquido posee en el punto 1 y 2 tres tipos de energías:

1.- Energía Cinética:

Donde:

Ec = Energía Cinética en Joules (J)

m = masa del líquido en Kilogramos (Kg)

v = velocidad del líquido en metros cada segundo (m/s)

2.- Energía Potencial:

Ep = mgh

Donde:

Ep = Energía Potencial en Joules (J)

m = masa del líquido en Kilogramos (Kg)

g = aceleración de la gravedad en metros cada segundo cuadrado (m/s²)

h = altura del líquido en metros (m)

3.- Energía de Presión:

Es originada por la presión de las moléculas entre sí. El trabajo realizado para el desplazamiento de las moléculas es igual a la Energía de Presión.

E_P = PV ó bien: E_P = P(m/ρ)

Así, de acuerdo al Teorema de Bernoulli, tenemos:

Ec₁ + Ep₁ + E_P1 = Ec₂ + Ep₂ + E_P2

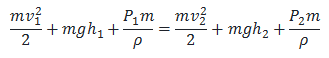
Si se divide la expresión anterior entre la masa, tendremos la expresión matemática del Teorema de Bernoulli.

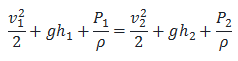
La Ecuación de Bernoulli señala que la suma de presión, energía cinética y energía potencial tienen el mismo valor en todos los puntos a lo largo de la corriente.

Restricciones  a la Ecuación de Bernoulli

No puede haber dispositivos mecánicos entre las dos secciones de interés. Aunque la Ecuación de Bernoulli es aplicable a una gran cantidad de problemas prácticos, existen algunas limitaciones que deben tener en cuenta con el fin de aplicar la Ecuación de manera correcta.

1.- Es válida solamente para fluidos incomprensibles, es decir, líquidos, puesto que el peso específico del fluido se tomó como el mismo en las dos secciones de interés.

2.- Agregar o eliminar, ya que la ecuación establece que la energía total de un fluido es constante.

3.- No puede haber transferencia de calor hacia dentro o fuera del fluido.

4.- No puede haber pérdidas de energía debido a fricción.

Aplicaciones del Teorema de Bernoulli

El teorema de Bernoulli se aplica cuando deseamos conocer la velocidad con la que sale un líquido a través de un orificio de un recipiente.

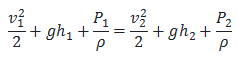
Para ello tendremos algunas consideraciones al aplicar la Ecuación de Bernoulli, tomando como ejemplo un recipiente abierto con una descarga en el punto más bajo de un costado.

En el siguiente dibujo, se muestran los dos puntos de referencia que sirven para comprender las consideraciones.

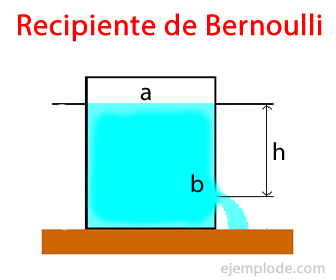
1.- La velocidad del líquido en el punto A es despreciable, comparada con la velocidad de salida del líquido en el punto B, es decir, se elimina el término:

v₁²/2

2.- El punto B se encuentra en el fondo del recipiente, a una altura cero sobre la superficie del fondo, podemos eliminar el término:

gh₂

3.- Como la energía de presión es provocada por la presión atmosférica y ésta es la misma tanto en A como en B, podemos eliminar los términos que corresponden a la Energía de Presión en dichos puntos:

P₁/ρ₁ y P₂/ρ₂

De acuerdo con lo anterior y despejando, la velocidad de salida del orificio (v₂) de la Ecuación de Bernoulli nos queda:

v = √2gh

Donde:

v = valor de la velocidad del líquido por el orificio en m/s

g = valor de la aceleración de la gravedad = 9.81 m/s²

h = profundidad a la que se encuentra el orificio de salida en m

La Ecuación anterior fue desarrollada por el Físico Evangelista Torricelli (1608-1647) y su teorema dice:

“La velocidad con la que sale un líquido por el orificio de un recipiente es igual a la que adquiriría un cuerpo que se dejara caer libremente desde la superficie libre del líquido hasta el nivel del orificio”.

Tubo de Pitot

Se utiliza para medir en una forma sencilla la velocidad de la corriente de un rio. El tubo tiene una forma de L y al ser introducido en la corriente, debido a la presión de ésta, el agua se elevará a cierta altura sobre la superficie. La velocidad se calcula empleando la fórmula del teorema de Torricelli, utilizando la altura que se obtiene del tubo.

Tubo de Venturi

Se utiliza para medir la velocidad de un líquido que circula a presión dentro de una tubería. Su funcionamiento también es una aplicación del Teorema de Bernoulli.

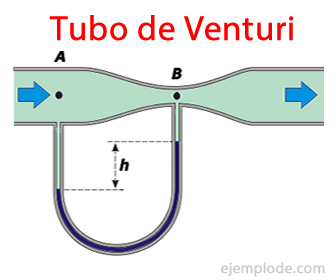
Cuando el líquido pasa por la sección más estrecha aumenta su velocidad, pero disminuye su presión. En los extremos de cada tubo se acoplan manómetros, así se conoce la presión, conociendo el valor de las áreas transversales se puede calcular la velocidad del líquido a través de la tubería si se utiliza la siguiente expresión, obtenida a partir de la ecuación de Bernoulli.

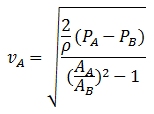
Ejemplos de Teorema de Bernoulli

El Tubo de Venturi se utiliza para medir la velocidad de un líquido que circula a presión dentro de una tubería. Su funcionamiento es una aplicación del Teorema de Bernoulli.

El tubo de Pitot se utiliza para medir en una forma sencilla la velocidad de la corriente de un rio.

El teorema de Bernoulli se aplica cuando deseamos conocer la velocidad con la que sale un líquido a través de un orificio de un recipiente.

El tubo de Pitot se utiliza para medir el flujo en una corriente de gas, que proviene de los hornos de Tostación.

El diseño del tubo de Venturi se utiliza en las Plantas Tratadoras de Aguas Residuales, para regular el flujo de las aguas que pasan del tratamiento primario al secundario.

El tubo de Pitot se añade al diseño de los aviones para tener una medida de la velocidad del aire que rodea al vehiculo.

El tubo de Venturi se emplea en la industria alimenticia para medir el flujo de bebidas como jugos y extractos.

El tubo de Pitot se utiliza en las salidas de los hornos donde se transforman las menas de Plomo en óxidos, para medir el flujo de óxidos de azufre.

El tubo de Venturi se utiliza en los trenes de purificación de agua, para medir el flujo de agua resultante que se va a depositar para servicio.

El tubo de Venturi se utiliza en las plantas de extracción de aceites para medición de las velocidades de los solventes y producto.