Ejemplo de Números Reales

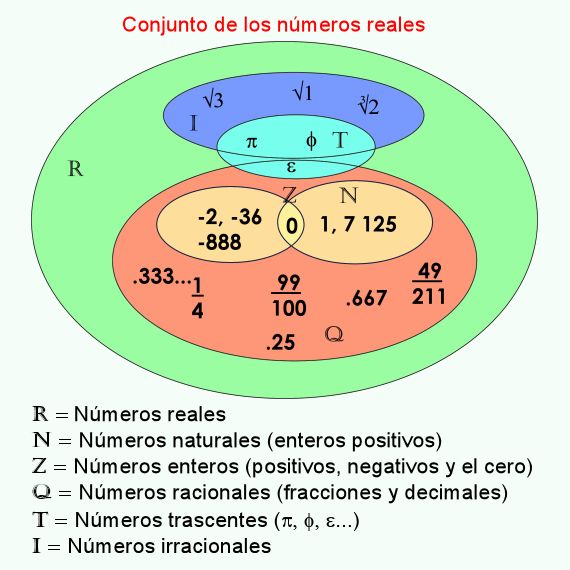
Los números reales son el conjunto de números sobre los que estudian las matemáticas, ya que son todos los números que pueden ser representados en una recta numérica. Como conjunto, los números reales contiene a los siguientes subconjuntos:

Los números enteros (Z), que a su vez está compuesto por:

Los números naturales (N): Son todos los números enteros positivos.
Los números negativos.
El cero.

Los números racionales (Q), que son todos los que se representan por un cociente o fracción, o por números decimales exactos o periódicos. Se dividen en:

Las fracciones, que expresan el cociente entre dos cantidades.
Los decimales, que expresan el resultado de un cociente fraccionario.

Los números irracionales (I), son los que expresan resultados numéricos cuyo resultado decimal no es periódico y se extiende al infinito.

Los números Trascendentes (T), son un subconjunto de los números irracionales y algunos racionales, que expresan relaciones matemáticas muy importantes, como la relación entre la circunferencia y el radio, el número pi (π).

Generalmente el conjunto de los números reales es representado por la letra “R”, y se les aplican las operaciones y las diferentes propiedades de operación estudiadas en aritmética y en álgebra:

• Suma.
• Resta.
• Multiplicación.
• División.
• Potenciación.
• Raíz.
• Propiedad Asociativa.
• Propiedad Conmutativa.
• Propiedad Distributiva.
• Propiedad de Cerradura.
• Elemento neutro.

Da clic en la imágen para ver más grande

Se puede definir a los números reales como el conjunto de todos los números con que realizamos operaciones matemáticas habitualmente en aritmética y álgebra. A Los números reales se contraponen los números imaginarios, que son todos aquellos que no pueden ser representados en una recta numérica, y que corresponden al producto b*i, donde b es un número real, y la constante i representa la raíz cuadrada de -1.

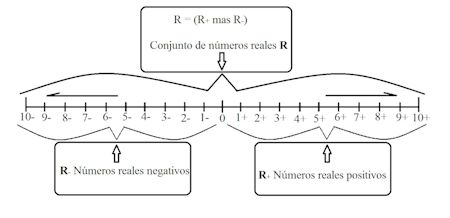
Los números reales en conjunto se representan por la letra R pero hay una subdivisión que contiene las dos siguientes:

1. Números reales positivos = R+
2. Números reales negativos = R-

Representando R+ a los números reales positivos, que en la recta numérica corresponden al positivo y que generalmente están a la derecha.
Representando R- a los números negativos, que en la recta numérica corresponden al negativo y que generalmente están a la izquierda. 

Ejemplo de números reales:

Números naturales (enteros positivos):

1
3
7
9
15
45
678
987
3456
2345
234567
384512
95732486
654821958
2468957888

Números enteros negativos:

 – 1
– 3
– 7
– 9
– 15
– 45
– 678
– 987
– 3456
– 2345
– 234567
– 384512
– 95732486
– 654821958
– 2468957888

Cero: 0

Números racionales:

Números fraccionarios:

½
–  ¼
14/35
2/7
5/9
2/3
– 4/7
6/9
9/15
45/99
65/85
– 77/88
12/101
1/125
4/222

Números decimales:

.25
0.999,
0.625
0.3333333….
0.1234512345…
0.625
0.11111
0.512
0.99
0.000001
0.0000000002
0.15348
0.000000000000000024
0.000100040002
0.5248

Números Trascendentales:

π = 3.14159265358979323846… (pi);
φ = 1.618033988749894848204586834365638117720309… (fi o número aureo)
ε = 2.7182818284590452353602874713527… (número de Euler)

Números irracionales:

√5
√2
√3
³√3
⁵√2
√7
√11
√101
⁴√99
⁷√12
³√9
⁵√33
⁷√2
⁴√4
³√122