Serie Aritmética

Una Serie Aritmética es la sumatoria de todos los términos de una Sucesión Aritmética. Si se trata de una Sucesión Aritmética infinita, se especifica hasta qué término se va a hacer la suma.

Una Serie es la suma de una Sucesión, y puede ser de dos tipos dependiendo del número de términos contenidos en la Sucesión:

Serie Finita: es la suma de una Sucesión Finita, es decir, que tiene un número establecido de términos. Por ejemplo:

{ 2 + 4 + 6 + 8 + 10 }

{ 3 + 6 + 9 + 12 + 15 }

{ 4 + 8 + 12 + 16 + 20 }

Serie infinita: es la suma de una Sucesión infinita, es decir, que tiene un número ilimitado de términos. Por ejemplo:

{ 2 + 4 + 6 + 8 + 10 + … }

{ 3 + 6 + 9 + 12 + 15 + … }

{ 4 + 8 + 12 + 16 + 20 + …}

La Serie Aritmética, siendo la suma de los términos de una Sucesión Aritmética, se puede calcular con las ecuaciones:

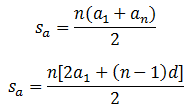
Donde:

s_a = Serie ó suma de los términos de la Sucesión Aritmética.

n = Número de términos que se van a sumar.

a₁ = Primer término de la Sucesión Aritmética.

a_n = Término que marca la última posición en la Sucesión.

d = Diferencia constante que se añade de un término a otro.

Ambas fórmulas son efectivas para conocer la suma de los términos de toda Sucesión Aritmética, hasta la posición que se requiera. Puede ser de los primeros cinco términos, de los primeros diez, o incluso de los primeros doscientos términos; los que sean.

Por su practicidad, es más utilizada la primera fórmula. Para conseguir utilizarla, es necesario primero obtener el término final a_n cuya posición se indica en el problema.

Ejemplos de Series Aritméticas

1.- De la Sucesión Aritmética { 5, 9, 13, 17,… } obtener la suma de los primeros 20 términos.

Primero obtenemos el término a₂₀:

a_n = a₁ + (n – 1)d

d = 9 – 5 = 4

a₁ = 5

n = 20

a₂₀ = (5) + (20 – 1)4

a₂₀ = 81

Ahora obtenemos la sumatoria desde a₁ hasta a₂₀:

s_a = [ n (a₁ + a_n) ] / 2

s_a = [ 20 (5 + 81) ] / 2

s_a = 860

2.- De la Sucesión Aritmética { 3, 10, 17,… } obtener la suma de los primeros 63 términos.

Primero obtenemos el término a₆₃:

a_n = a₁ + (n – 1)d

d = 10 – 3 = 7

a₁ = 3

n = 63

a₆₃ = (3) + (63 – 1)7

a₆₃ = 437

Ahora obtenemos la sumatoria desde a₁ hasta a₆₃:

s_a = [ n (a₁ + a_n) ] / 2

s_a = [ 63 (3 + 437) ] / 2

s_a = 13860

3.- De la Sucesión Aritmética { 3, -1, -5,… } obtener la suma de los primeros 13 términos.

Primero obtenemos el término a₁₃:

a_n = a₁ + (n – 1)d

d = -1 – 3 = - 4

a₁ = 3

n = 13

a₁₃ = (3) + (13 – 1)(-4)

a₁₃ = -45

Ahora obtenemos la sumatoria desde a₁ hasta a₁₃:

s_a = [ n (a₁ + a_n) ] / 2

s_a = [ 13 (3 - 45) ] / 2

s_a = -273

4.- De la Sucesión Aritmética { ½, ¾ , 1,… } obtener la suma de los primeros 12 términos.

Primero obtenemos el término a₁₂:

a_n = a₁ + (n – 1)d

d = ¾ – ½ = ¼

a₁ = ½

n = 12

a₁₂ = (1/2) + (12 – 1)(1/4)

a₁₂ = 13/4

Ahora obtenemos la sumatoria desde a₁ hasta a₁₂:

s_a = [ n (a₁ + a_n) ] / 2

s_a = [ 12 ( ½  + 13/4) ] / 2

s_a = 22 ½

5.- De la Sucesión Aritmética { 7, 10, 13,… } obtener la suma de los primeros 9 términos.

Primero obtenemos el término a₉:

a_n = a₁ + (n – 1)d

d = 10 – 7 = 3

a₁ = 7

n = 9

a₉ = (7) + (9 – 1)3

a₉ = 31

Ahora obtenemos la sumatoria desde a₁ hasta a₉:

s_a = [ n (a₁ + a_n) ] / 2

s_a = [ 9 (7 + 31) ] / 2

s_a = 171

6.- De la Sucesión Aritmética { 3, 14, 25,… } obtener la suma de los primeros 21 términos.

Primero obtenemos el término a₂₁:

a_n = a₁ + (n – 1)d

d = 14 – 3 = 11

a₁ = 3

n = 21

a₂₁ = (3) + (21 – 1)11

a₂₁ = 223

Ahora obtenemos la sumatoria desde a₁ hasta a₂₁:

s_a = [ n (a₁ + a_n) ] / 2

s_a = [ 21 (3 + 223) ] / 2

s_a = 2373

7.- De la Sucesión Aritmética { -10, -6, -2,… } obtener la suma de los primeros 80 términos.

Primero obtenemos el término a₈₀:

a_n = a₁ + (n – 1)d

d = -6 – (-10) = 4

a₁ = -10

n = 80

a₈₀ = (-10) + (80 – 1)4

a₈₀ = 306

Ahora obtenemos la sumatoria desde a₁ hasta a₈₀:

s_a = [ n (a₁ + a_n) ] / 2

s_a = [ 80 (-10 + 306) ] / 2

s_a = 11840

8.- De la Sucesión Aritmética { -5, -13, -21,… } obtener la suma de los primeros 50 términos.

Primero obtenemos el término a₅₀:

a_n = a₁ + (n – 1)d

d = -13 – (-5) = (-8)

a₁ = -5

n = 50

a₅₀ = (-5) + (50 – 1)(-8)

a₅₀ = -397

Ahora obtenemos la sumatoria desde a₁ hasta a₅₀:

s_a = [ n (a₁ + a_n) ] / 2

s_a = [ 50 (-5 -397) ] / 2

s_a = -10050

9.- De la Sucesión Aritmética { 2, 7, 12,… } obtener la suma de los primeros 14 términos.

Primero obtenemos el término a₁₄:

a_n = a₁ + (n – 1)d

d = 7 – 2 = 5

a₁ = 2

n = 14

a₁₄ = (2) + (14 – 1)5

a₁₄ = 67

Ahora obtenemos la sumatoria desde a₁ hasta a₁₄:

s_a = [ n (a₁ + a_n) ] / 2

s_a = [ 14 (2 + 67) ] / 2

s_a = 483

10.- De la Sucesión Aritmética { 10, 21, 32,… } obtener la suma de los primeros 46 términos.

Primero obtenemos el término a₄₆:

a_n = a₁ + (n – 1)d

d = 21 – 10 = 11

a₁ = 10

n = 46

a₄₆ = (10) + (46 – 1)11

a₄₆ = 505

 Ahora obtenemos la sumatoria desde a₁ hasta a₄₆:

s_a = [ n (a₁ + a_n) ] / 2

s_a = [ 46 (10 + 505) ] / 2

s_a = 11845