Vectores
En Matemáticas, y también para aplicaciones en Física, un vector es un segmento que tiene una orientación. Un vector AB queda determinado por dos puntos, llamados Origen A y Extremo B; y consta de tres elementos básicos, llamados Módulo, Dirección y Sentido, que se explicarán a continuación.
El Módulo de un Vector es la distancia que separa a A de B, y se designa por el vector entre barras:
![]()
La Dirección del Vector es la dirección de la recta en la que se encuentra el vector y la de todas sus paralelas. Más sencillo, es la inclinación que tiene.
El Sentido de un Vector está determinado por cómo se trace; es si va de A a B o de B a A.
Dos Vectores están en condición de igualdad si tienen el mismo Módulo, Dirección y Sentido. Ambos quedarán como representantes de un único vector.
Se llamará Representante Canónico a aquel Vector que tiene por origen el punto central del plano cartesiano.
Para su Notación, los vectores son representados por letras:
![]()
O bien mediante uno de sus representantes, designando su origen y su extremo con una flecha encima:
![]()
Contenido del artículo
Producto de un Vector por una Constante
Cuando se multiplica una constante (un número cualquiera) k por un vector v, el resultante es otro vector:
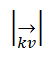
Que tendrá un Módulo igual al producto del módulo del Vector v por el valor absoluto de k:
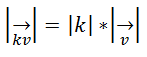
Su Dirección será la misma que tiene v en el principio.
Su Sentido va a ser el mismo de v si k>0. Y el Sentido será el opuesto de v si k<0.
En el caso del producto Cero 0, que es cuando se multiplica el Vector v por Cero, el resultado es igual al Vector Cero:
![]()
Las propiedades del Vector Cero son que su origen y extremo coinciden y, por tanto, su módulo es cero y carece de dirección y de sentido.
En el caso del producto por -1, el Vector resultante se llamará Opuesto de v, y se designará por:
![]()
Suma de Vectores
Dados dos vectores “u” y “v”, para sumarlos gráficamente hay dos posibilidades:
La primera es situar el origen del segundo vector sobre el extremo del primero y el vector suma es el vector que une el origen del primero con el extremo último.
La segunda es situar los dos vectores, uniéndolos en un origen común. Se forma el paralelogramo que tiene por lados los dos vectores y la diagonal que parte del origen de los dos vectores es el Vector Resultante.
Diferencia de Vectores
La Resta o Diferencia de Vectores se puede interpretar como sumar al primer Vector, el Opuesto del segundo.
![]()
Combinación lineal de Vectores
Existiendo dos vectores “u” y “v”, y dos números “a” y “b”, el vector resultante “au + bv” es denominado una Combinación lineal de “u” y “v”.
Cabe destacar que cualquier vector se puede poner como combinación lineal de otros dos, y que esta combinación lineal es única.
Coordenadas de un Vector
Dos vectores “u” y “v” con diferentes direcciones, y con un módulo diferente de cero, forman una base, ya que cualquier vector del plano se puede poner como combinación lineal de ellos.
Si los dos vectores de la base son perpendiculares entre sí, se dice que forman una base ortogonal, y si además tienen módulo con valor unidad, se asume que forman una Base Ortonormal.
Para conocer las Coordenadas de un Vector respecto de una base:
Cualquier vector w se puede poner como combinación lineal de los elementos de una base B(x,y) de la siguiente forma:
![]()
A los números (a,b) se les llama coordenadas de w respecto de B.
Y se va a expresar de dos posibles maneras:
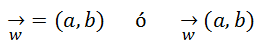
Operaciones matemáticas con Coordenadas
Se puede ejecutar operaciones con las coordenadas de los vectores, de una manera bastante sencilla.
Para la Suma, las coordenadas del Vector Resultante u + v se obtienen sumando las coordenadas de u con las de v:
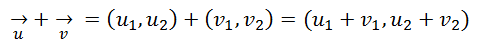
Para la Resta, las coordenadas del Vector Resultante u – v se obtienen con la diferencia de las coordenadas de u y v.
![]()
Para el Producto de un Vector por un número, las coordenadas del vector ku se obtienen multiplicando por k las coordenadas de u:
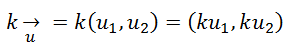
Y ahora, para ejecutar la Combinación Lineal de Vectores, se aplica lo siguiente:
![]()
Producto Escalar de Vectores
El producto escalar de dos vectores “u” y “v” es un número resultante de multiplicar el módulo de cada uno de los vectores por el coseno del ángulo que forman, y se presenta de la siguiente forma:
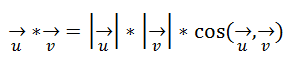
El producto Escalar tiene propiedades bien definidas, muy similares a las establecidas para los números, tal cual.
El producto Escalar del Vector Cero por otro Vector cualquiera es el número 0.
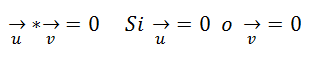
Si dos Vectores son Perpendiculares, entonces su producto escalar es cero:
![]()
El Producto Escalar de dos vectores es igual al producto de uno de ellos por la proyección del otro sobre él, con signo positivo o negativo, según si forman un ángulo agudo u obtuso.
Propiedad Conmutativa:
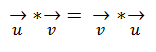
Propiedad Asociativa:
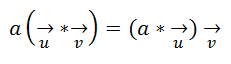
Propiedad Distributiva:
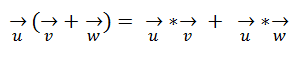
Si B(x,y) es una Base Ortogonal:
![]()
Si B(x,y) es una Base Ortonormal:
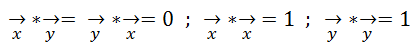
¿Cómo citar? Contreras, V. & Del Moral, M. (s.f.). Vectores.Ejemplo de. Recuperado el 26 de Septiembre de 2023 de https://www.ejemplode.com/5-matematicas/4619-vectores.html
