Ejemplo de Derivadas

La Derivada es la expresión matemática que describe el cambio de una variable, que es función de una variable independiente que se cuenta como principal.

Las Derivadas son la base de funcionamiento del Cálculo Diferencial, creado por Sir Isaac Newton, el célebre matemático y físico inglés, bajo el nombre original de Fluxiones.

Para comprender mejor el concepto de la Derivada, es necesario definir los Incrementos.

Los Incrementos

El Incremento de una variable que pasa de un valor numérico a otro es la diferencia que se obtiene comparando el valor inicial y el final. Un incremento de la variable “x” se representa por el símbolo “Δx”, que se lee “delta x”.

El incremento puede ser positivo o negativo, según que la variable aumente o disminuya al cambiar de valor. De este mismo modo:

Para continuar con la explicación, se toma como referencia y=f(x), que representa a “y” como una función de “x”. Si en y=f(x) la variable independiente “x” toma un incremento “Δx”, entonces “Δy” indicará el incremento correspondiente de la función “f(x)”.

El incremento “Δy” siempre ha de contarse desde el valor inicial definido de “y”, que corresponde al valor inicial fijado de “x”, desde el cual se cuenta el incremento “Δx”.

Por ejemplo, si se toma como valor inicial x=10, y la función es y=x², el valor de “y” quedará como (10)²=100. En resumen, los valores iniciales son: x=10, y=100.

Y suponiendo que haya un incremento de “x” hasta el valor de x=12, el incremento será Δx=2, comparando con el x=10 inicial. De este modo, el valor de “y” quedará como (12)²=144, siendo el incremento de Δy=44, comparando con el y=100 inicial.

En resumen, los nuevos valores son: x=12, y=144. Los incrementos son: Δx=2, Δy=44.

Y como segundo caso, suponiendo que haya un incremento negativo de “x” hasta el valor de x=9, el incremento será Δx=-1, comparando con el x=10 inicial. De este modo, el valor de “y” quedará como (9)²=81, siendo el incremento de Δy=-19, comparando con el y=100 inicial.

En resumen, los nuevos valores para el segundo caso son: x=9, y=81. Los incrementos son: Δx=-1, Δy=-19.

Hay veces que será posible que “y” tenga signo contrario al de “x”. Todo depende de la función.

Comparación de Incrementos

Se seguirá tomando como referencia la función y=x². Supongamos que se parte de los valores iniciales “y” y “x”. Entonces daremos un incremento a cada una de las variables, escribiéndolo así:

Ahora, para encontrar la razón de los incrementos, es decir, la relación que hay entre ellos, debemos obtener Δy/Δx:

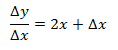
Ya asignando un valor a x, por ejemplo x=4, se calculará el límite cuando Δx tiene tendencia al valor cero 0. El límite será, por así decirlo, el valor tope que tendrá si progresivamente se inclina al valor cero, hasta llegar a él.

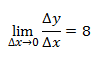
En la siguiente tabla se representan los incrementos y las relaciones de los incrementos de las variables “x” y “y”.

Se va notando en la tabla que cuanto más pequeño es el incremento Δx, más se aproxima Δy al valor 8, que es el límite calculado previamente.

Derivada de la función de una variable

La definición fundamental del Cálculo Diferencial es la que sigue:

“La Derivada, llamada Coeficiente Diferencial o Función Derivada, de una función, es el límite de la razón del incremento de la función al incremento de la variable independiente cuando éste tiende a cero”.

Cuando el límite de esta razón existe, se dice que la función es Derivable o que Tiene Derivada.

La definición se puede dar mediante símbolos en la forma siguiente:

Dada la  función y=f(x), se considerará un valor inicial fijo de x.

Se da a “x” un incremento “Δx”; entonces se obtiene para la función “y” un incremento “Δy”, siendo el valor final de la función:

Para hallar el incremento de la función, se resta la función de trabajo y=f(x) de la incrementada.

Dividiendo los dos miembros por Δx, incremento de la variable independiente, resulta:

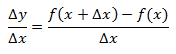
El límite del segundo miembro cuando Δx tiende al valor cero es, por definición, la Derivada de f(x), es decir, de “y”. Y se representa por el símbolo dy/dx. Así que la igualdad siguiente define la derivada de “y” con respecto a “x”.

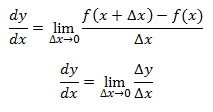
Ya simplificada, queda la última expresión.

La operación de hallar la Derivada de una función se llama Derivación.

Regla General para la Derivación

El procedimiento para calcular la derivada de una función y=f(x) se puede resumir a cuatro sencillos pasos:

Primer Paso: Se sustituye, en la función, “x” por “x+Δx”, y se calcula el nuevo valor de la función “y+Δy”.

Segundo Paso: Se resta el valor dado de la función del nuevo valor, y se obtiene Δy (incremento de la función).

Tercer Paso: Se divide Δy (incremento de la función) por Δx (incremento de la variable independiente)

Cuarto Paso: Se calcula el límite de este cociente cuando Δx (incremento de la variable independiente) tiende a cero. El límite así hallado es la derivada buscada.

Estos cuatro pasos aplican a todas las funciones derivables.

Ejemplos de Fórmulas para obtener Derivadas

Como el procedimiento de los cuatro pasos de la Regla General para la Derivación resulta muy tardado, se han establecido fórmulas y reglas que se pueden usar en la función que aplique a su caso.

No olvides dejar tus comentarios.