Inicio > Matemáticas > Simplificación de radicales

Ejemplo de Simplificación de radicales

Las expresiones de la forma bn nos representan a un número único, al que llamamos raíz principal enésima de b y como se menciona antes hay casos en los que es más ventajoso expresar la cantidad con un radical en lugar de usar exponentes fraccionarios.

Las leyes de los radicales se desprenden de las leyes de los exponentes  ya generalizadas, y es necesario tenerlas presentes al trabajar con radicales. Recuerde que
 
bn =b 1/n y si n es par ⇒ b > 0
 
Aprovechando estas leyes de los radicales puede cambiarse la forma radical de las siguientes maneras:

a) Quitar del radicando las potencias múltiplo del índice, para lo cual factorizamos antes.
 


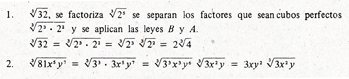
b) Reducir el índice del radical, sin olvidar que el radicando debe ser positivo.
 

 
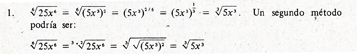
c) Racionalizar el deneminador. Racionalizar significa reemplazar la expresión por una equivalente sin radical en donde indique.
 
 
Se busca un factor (z) tal que haga que el radicando en el denominador tenga un exponente mútiplo del índice del radical y usando el teorema x/y = xy  / yz se efectúa el producto.
 
EJEMPLO SIMPLIFICACIÓN DE RADICALES:
 
 

 


Keywords: Ejemplo de Simplificación de radicales, Simplificación de radicales, ,
Creado por: Ana el 12.08.08

Si no encontraste lo que buscabas, prueba la búsqueda:

Búsqueda personalizada

Ejemplos relacionados


Últimos 10 comentarios en Ejemplo de Simplificación de radicales

nathaly
10.08.10 a las 19:50:10
gracias por que e aprendido mucho pero mucho mas
kas
05.20.10 a las 23:20:01
no me sirvio de mucho pero entendi algo nuevo
ronal
05.02.10 a las 20:52:44
no me gusto porque no se entendio
maloenmatematicas
04.05.10 a las 12:28:00
soy extemadamente malo en esto =(
fer
02.09.10 a las 22:58:37
muy buena teoria. y por lo poco que puedo distinguir los ejemplos son erbuenos, en lo personal no distingo los radicando deberian agrandar el tamaño de los numeros. de todas formas gracias
mery
11.26.09 a las 17:21:59
es muy BUEN ejenplo y nos sirve de ayuda para las actividades ¿GRACIAS?
elizabet
10.05.09 a las 9:16:01

hola
esta muy bien lo ke explica nadamas lo que pasa es que de enjemplos y definiciones de lo que es un radical,radicando,la raiz,el indice, y el exponente es decir que muestren una expresion alegrabica e indique cual es cada uno de ellos
Caren
06.24.09 a las 17:14:38
sera que me podrian ayudar con unos problema de simplificacion son:
2/108 1/2 /8
la diagonal es simbolo de raiz cuadrada, esperare su respuesta
irela
04.28.09 a las 9:53:33
muchas graciasias por ayudarme ok no le entendia y ahora si
bianca
01.22.09 a las 18:05:52
gracias x alludarme mucho en esto de los radicales

Deja un comentario en Ejemplo de Simplificación de radicales

 Nombre *
Correo *
Captcha