Ejemplo de Fuerza

En física, la fuerza es una magnitud vectorial, es decir, que puede representarse gráficamente mediante un vector, que indica su punto de aplicación, intensidad, dirección y sentido y su definición y propiedades están relacionadas con la masa y el movimiento de los objetos.

En la física dinámica, la fuerza es una de las magnitudes que estudian y definen las leyes de Newton. Para que exista o para que se detenga un movimiento, se debe aplicar una fuerza. El movimiento producirá una aceleración que depende tanto de la fuerza aplicada, como de la masa del objeto. La fórmula básica dice que la fuerza es el resultado de multiplicar la masa del objeto por la aceleración que adquiere.

La masa de un objeto es la relación entre su volumen y su densidad, y se mide en gramos. La aceleración es la relación entre la distancia que recorre el cuerpo y el tiempo que tarda en recorrer esa distancia. La aceleración se mide en metros por segundo. La fuerza es el producto de la masa multiplicada por la aceleración del cuerpo, el resultado que se obtiene se mide con la unidad llamada Newton, que se define como la fuerza necesaria para hacer que un objeto de un kilogramo de peso, alcance una aceleración de 1 m/s².

F = m*a

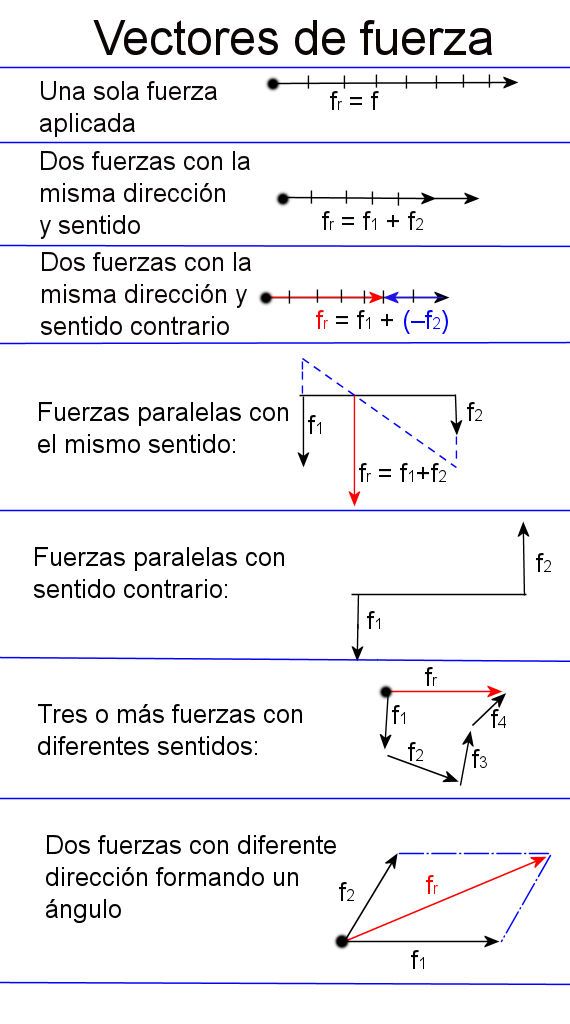
Al hablar de fuerzas vectoriales, podemos representar gráficamente una o más fuerzas que actúan sobre un objeto, y calcular y representar sus resultantes. Generalmente se considera que las líneas que indican el sentido son positivas si se dirigen a la derecha o hacia arriba, y negativas si se dirigen a la izquierda o hacia abajo. 

1. El caso más sencillo es cuando actúa una fuerza, sobre el objeto. Tendrá un punto de aplicación, una intensidad, una dirección, y un sentido. En este caso, como sólo actúa una fuerza, la fuerza resultante será igual a la fuerza aplicada: fr = f.
2. Otro caso es cuando actúan dos o más fuerzas sobre el objeto, las cuales tienen diferente intensidad, pero el mismo punto de aplicación, la misma dirección y el mismo sentido. Fr = f1+f2+f3…+fn.
3. Una variante es cuando actúan dos o más fuerzas sobre el objeto, con diferente intensidad, mismo punto de aplicación, misma dirección, pero sentidos contrarios. Si bien se aplica la misma fórmula, la suma de fuerzas de sentido negativo equivale a restar esas fuerzas. Fr = f1+f2+f3…+fn.
4. Dos fuerzas angulares. En este caso, se aplican dos fuerzas sobre el objeto, las cuales tienen el mismo punto de aplicación, diferente dirección y el mismo sentido. Para resolver la fuerza y la dirección de la resultante, se usa el método del paralelogramo, que consiste en tratar líneas paralelas a ambas fuerzas, y la diagonal entre el punto de aplicación y el punto de intersección de las paralelas será la resultante.
5. Tres o más fuerzas angulares. Cuando a un objeto se le aplican tres o más fuerzas, la resultante se obtiene trazando un polígono, formado por cada una de las fuerzas aplicadas, comenzando por la fuerza 1. Donde termina el trazo, se agrega la fuerza 2, con la misma dirección y sentido con que se trazó, pero teniendo como punto de origen el final del trazo de la fuerza 1, el vector 3 comenzando en el punto final del vector 2, y así sucesivamente con todos los vectores. La resultante será el vector que se forme entre el punto de aplicación y el final del vector de la última fuerza aplicada.
6. Fuerzas paralelas con el mismo sentido. En ellas se aplican dos fuerzas paralelamente, como cuando jalamos una barra, y en este caso, mediante los vectores podemos calcular la fuerza resultante y el punto de aplicación.
7. Fuerzas paralelas de sentido contrario. En este caso, hay dos posibilidades: fuerzas de diferente magnitud. En este caso, se puede determinar el punto de aplicación y la fuerza resultante. Fuerzas de igual magnitud. También llamado par de fuerzas, en este caso, las fuerzas no tienen resultante, sino un movimiento de rotación alrededor del centro de la distancia donde se aplican las fuerzas.

La fuerza aplicada a un objeto, produce movimiento que será mayor o menor dependiendo de su masa. Cuando un objeto está en reposo, la fuerza con la que actúa es igual a cero, ya que, al no existir movimiento, esta componente es igual a cero, y toda cantidad multiplicada por cero, da como resultado cero.

Para imprimirle movimiento, debemos aplicar una fuerza, que producirá un movimiento proporcional a la masa del objeto.  Si aplicamos la misma fuerza a dos objetos con diferente peso, la aceleración será diferente. El objeto más ligero, tendrá mayor aceleración que el objeto más pesado:

F= 0.5N 

Objeto 1 = 85 gramos.

Objeto 2 = 125 gramos.

Calculamos la velocidad de cada objeto. Primero convertimos las medidas de la masa de cada objeto en kilogramos:

Objeto 1 = 85 gramos = 0.085 kg.

Objeto 2 = 125 gramos. = 0.125 kg.

Ahora dividimos la fuerza aplicada entre la masa de cada objeto, y el resultado será su aceleración en metros por segundo:

v = F/m = 0.5 / 0.085 = 5.88 m/s

v = F/m = 0.5 / 0.125 = 4 m/s 

Como vemos, con una misma fuerza, el objeto más ligero adquiere una mayor aceleración que el objeto más pesado.

Ejemplos de fuerza

1. Calcular la fuerza aplicada a un objeto de 450 gramos, que alcanza una velocidad de 75 cm/s.

Primero convertimos la masa en kg, y la velocidad en metros por segundo:

m = 450 g = 0.45 kg

v = 75 cm/s = 0.75 m/s

F= mv = 0.45 * 0.75 = 0.3375 N

2. Calcular la velocidad que tendrán dos objetos cuyas masan son de 600 gramos y de 800 gramos, al aplicárseles una fuerza de 0.4N

Calculamos la velocidad del primero objeto:

F = 0.4 N

m = 0.600 kg

v = F/m = 0.4 / 0.6 = 0.6667 m/s

Calculamos el segundo objeto:

F = 0.4 N

m = 0.800 kg

v = F/m = 0.4 / 0.8 = 0.5 m/s

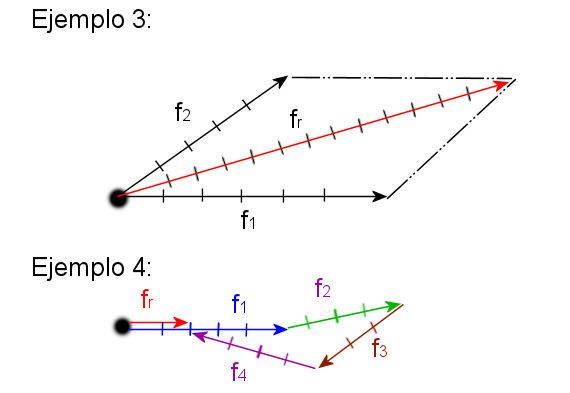
Dibujar el vector de dos fuerzas que actúan con un objeto. La primea, con dirección horizontal y sentido positivo, con una fuerza de 6 N, y la otra una fuerza de 5 N, con sentido positivo y una dirección con un ángulo de 40° respecto a la primera.

3. Dibujar el vector de 4 fuerzas que actúan sobre un objeto, con las siguientes características:

F1 = 5 N, 0°, hacia la derecha.

F2 = 4 N, 30°, hacia la derecha y hacia arriba

F3 = 3 N, 60°, hacia la izquierda y hacia abajo

F4 = 4 N, 30°, hacia la izquierda y hacia arriba